Time Dilation

This article will be based off of ideas presented in the quick piece "Special Relativity" in my relativity section. Go check that out before you read this if you want some background. The entire article will give you a good grasp on the topic of time dilation, but skip to the bolded and italicized sentence for a quick explanation to save some time.

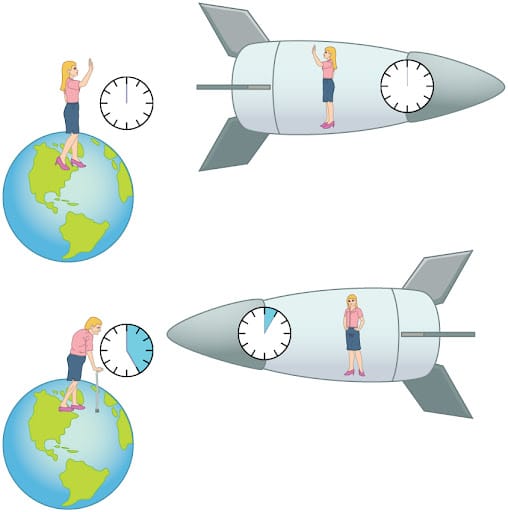
Picture this: You are standing on a stationary planet. Let's ignore the fact that its solar system, galaxy, and whatnot might be moving. You have excellent vision and are watching your friend, Bob, fly by very quickly inside of a clear rocket. Above Bob is a mirror, and he is holding a flashlight in his hand. From Bob's point of view, he is stationary in the rocket. He shines the flashlight straight up, and the light bounces straight back down to him. From your point of view, however, the light actually traveled diagonally in his direction of motion because the rocket is moving.

For another example, imagine you are watching a train go by. Bob is inside of it. He throws a ball up and it lands back in his hands. You see the ball take an arc-shaped path because the train is moving, while he sees it go straight up and back down into his hands because from his point of view, he is simply standing in the train car that he views at rest.

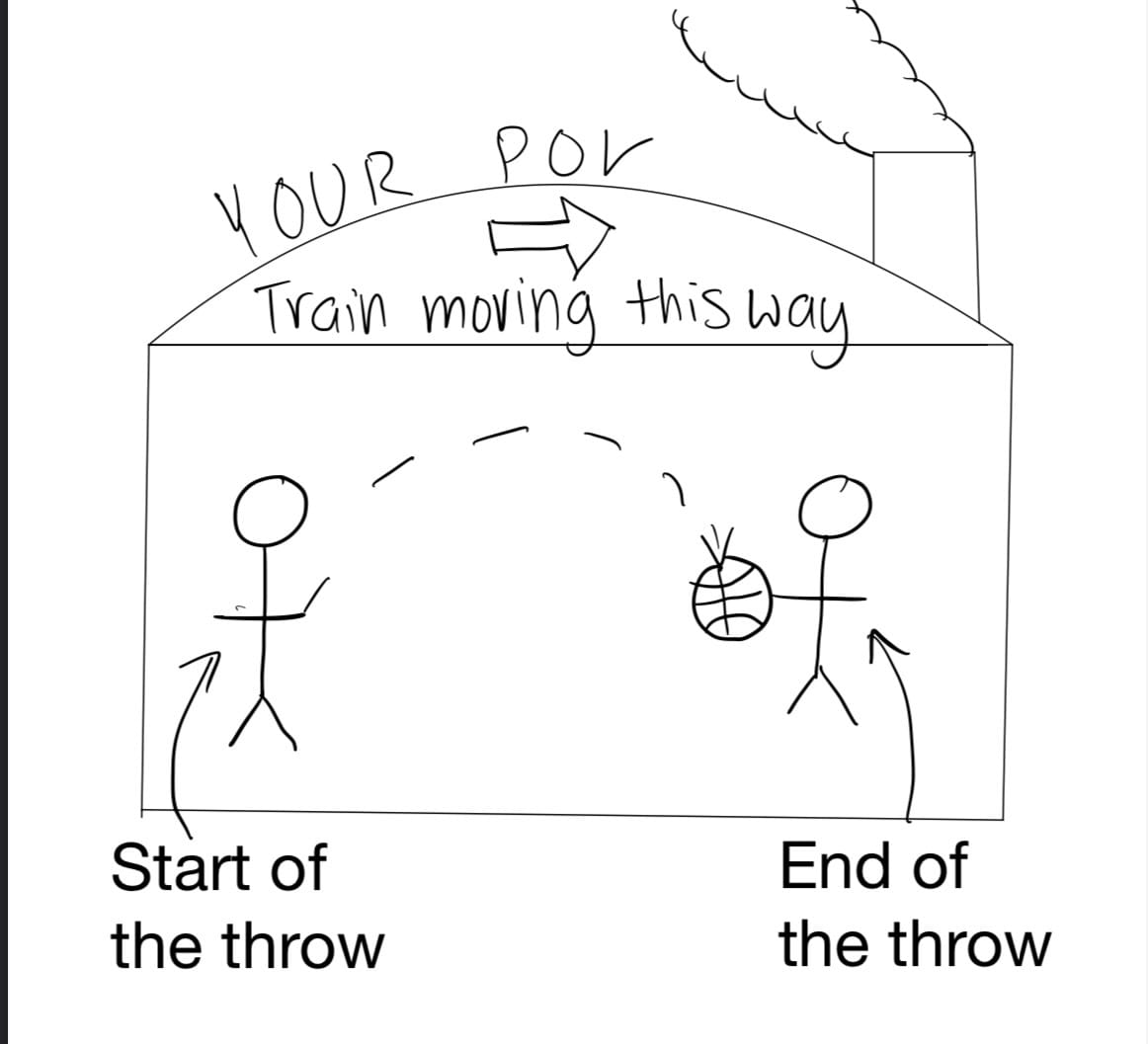
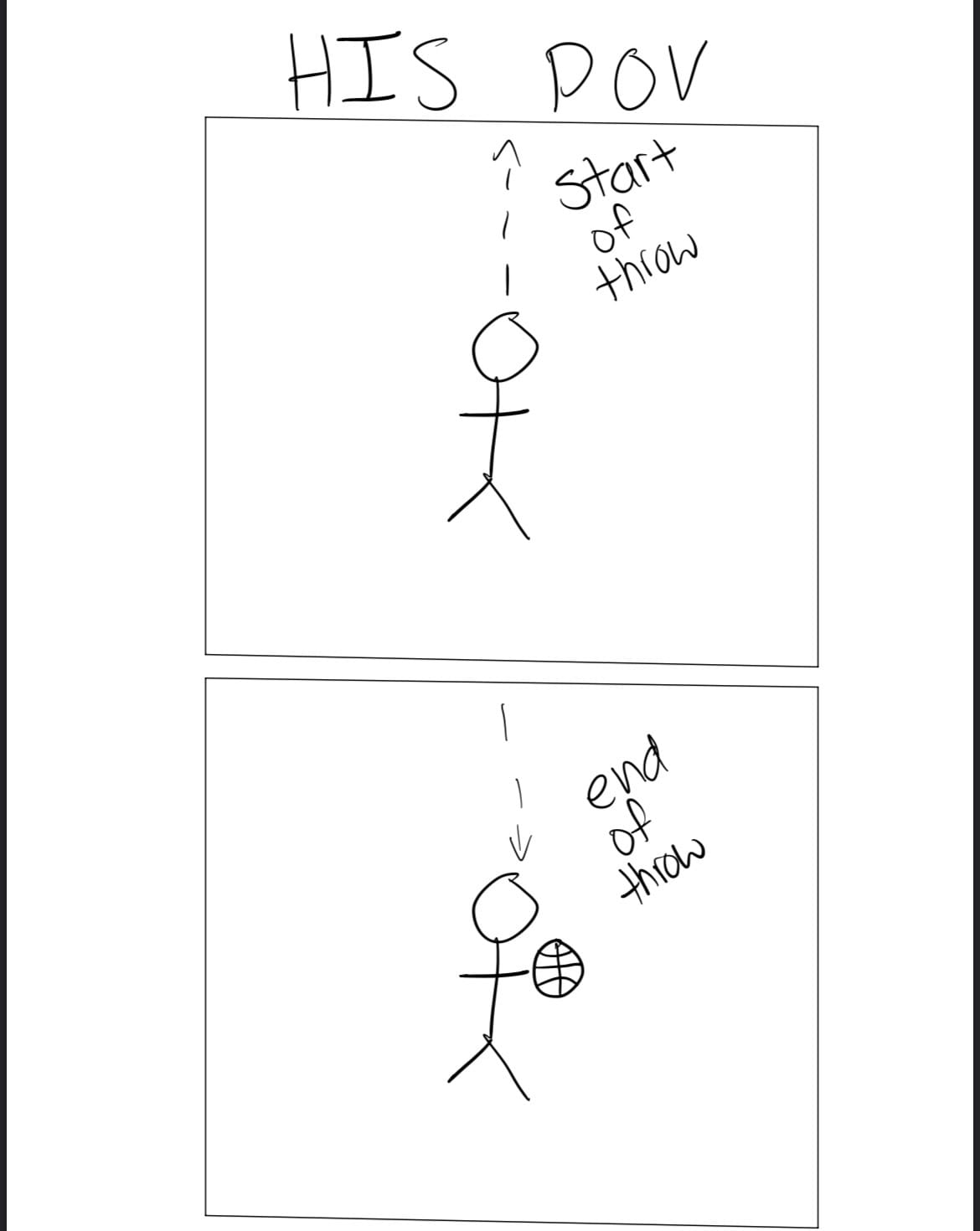
This same discrepancy happens between you and Bob on the spaceship.

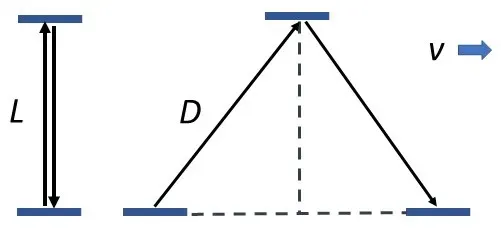
The left diagram is Bob's point of view: He sees the light go straight up and back down. The right diagram is your point of view: Because the spaceship and mirror are moving horizontally, the light must also move horizontally in order to bounce off the mirror and back into Bob's eyes.

Clearly, the light seems to travel to different distances. The left distance is noticeably shorter than the right one. However, according to Einstein, the speed at which light covers these distances must be the same.

Physics tells us that the distance something travels equals its speed multiplied by the amount of time spent in travel. For example, if you go 100 miles per hour for 3 hours, you go 300 miles. If you go 100 miles an hour for half an hour, you go 50 miles.

Since the distance that the light travels seems to be different, but the speeds are the same, the TIME light spends traveling must be different in each situation. To illustrate this, say you are going 100 miles an hour again. If you want to go 200 or 100 miles, you must spend different amounts of time traveling.

So, what conclusion can we draw from this?

If you and Bob time his light's back and forth travel, your recorded time will be greater than his because you see his distance as greater but the same speed.

This part, to me, was pretty intuitive and understandable. It took me more time to realize how this meant that everything else also experienced time in a different way. How do clocks slow down and humans age slower?

This explanation isn't based off of the above and is one that I actually haven't seen before (although I'm sure many others have already come up with it).

Again, imagine you are sitting on a stationary planet. In front of you, your friend Bob is flying by in a rocket that is going very close to the speed of light. Luckily, there is a huge window on the rocket so you can see Bob. Bob points a light beam straight ahead of him, which is also in the direction of motion of the rocket.

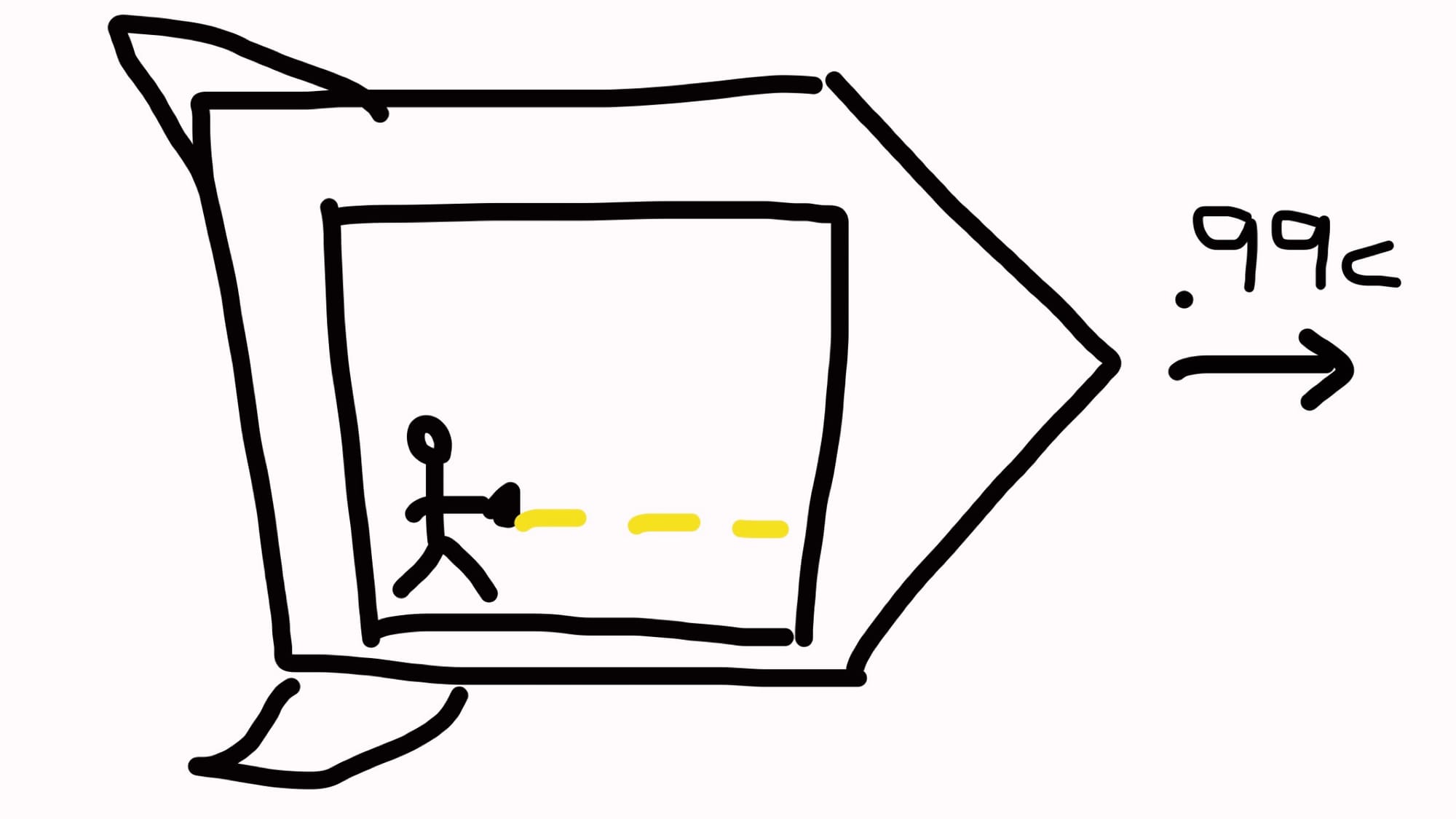
Since the rocket is moving very close to the speed of light, the light beam will seem to crawl from the back of the rocket to the front of it.

For example, if Bob threw a 500 mile per hour baseball (ignoring the addition of velocities) and the rocket is flying at 501 miles per hour, the ball would take quite a while to reach this long rocket.

The same is essentially true for light. However, from Bob's point of view, the light was super fast and zipped to the front of the rocket in no time. Since we know Bob isn't lying, we conclude that the light is almost infinitely faster than Bob.

In order for this fact to stay consistent with your perspective, on the planet, you must perceive Bob as incredibly slow so that the slow light still seems infinitely faster than him.

While clocks or people aren't constantly shooting light beams in rockets, the conclusions drawn from these examples show that they will still seem much slower in time from our point of view.